750-G. New Year and Binary Tree Paths

2021-03-16 23:58:21 +0800 CST Tags: binary-tree, dp

出處：https://codeforces.com/contest/750/problem/G
提交：https://codeforces.com/contest/750/submission/107138494

問題：給定一棵 index 從 1 開始向下無限延伸的二元樹，請問在這棵樹裡面有幾條不同的路徑，它們各自經過的節點索引值總和恰好都是一個給定的整數 $s\in[1,10^{15}]$。

解法：這題給定的參考作法 [1] 是同時枚舉一棵子樹之左右兩樹枝的長度 L 和 R (可簡單估算上界大約都落在 50，為了保險起見可估 55)，並推得在固定 L 和 R 之下的子樹若要符合總和 s 的話會有一個唯一 [2] 的 LCA (最低公共祖先，Lowest Common Ancestor) 我們姑且稱之為 x，給定 x 之後就可以推算出這棵子樹隨著樹枝擺動的左右葉子節點它們各自的浮動範圍，姑且分別稱之為 $a\in[.]$ 和 $b\in[.]$。由於在二元樹內從 1 走到節點 n 的總和根據公式 [3] 為 2n - popcount(n)，其中 popcount 指的是一個整數有多少個 1-bit，因此有了 x、a、b，這棵子樹的總和便為 2a - popcount(a) + 2b - popcount(b) - 2 * (2x - popcount(x)) + x 而且它必須 = s。要知道這個方程式的解數量，必須採用 digit DP 技巧 [4]，但此時 a 和 b 的範圍仍然不是從 0 起算，這樣會造成實作上的困難，所以根據下面程式碼註解說明，我們把 a 拆成 baseA + dA、把 b 拆成 baseB + dB，使得 dA 和 dB 都是從 0 起算，於是這個式子可以轉成 2 (dA + dB) = s+3x-2(baseA+baseB)+(R>=1) + popcount(dA)+popcount(dB)，再每次固定住 $\text{popcount}(dA)+\text{popcount}(dB)\in[0,\ \max(0,L-1) + \max(0, R-1)]$ 去得到這個條件下所有合法 (dA, dB) 的數量，其中 $dA\in[0,2^{\max(0,L-1)})$ 而且 $dB\in[0,2^{\max(0,R-1)})$。最後把不同 L 和 R 底下的答案加起來就是我們要的。

附註：
[1] https://codeforces.com/blog/entry/49412
[2] 這張圖說明 L=2、R=3 的時候 x=3 的樹的總和必定小於 x=4 的樹的總和，因為上三角 3、6、7 分別小於 4、8、9，然後除了這些節點之外，如果小樹節點與對應的大樹節點差距至少為 2，那麼小樹節點往右下方跑之後的值和大樹節點往左下方跑之後的差距仍然至少為 2，所以兩樹的節點彼此之間可以一一對應而且維持一定的大小關係，加總之後亦然。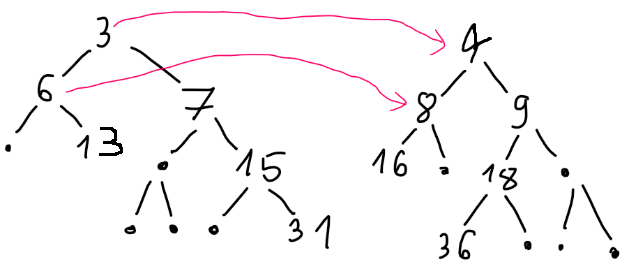
Example image
[3] 這個公式的證明很簡單，數學歸納法即可。假設從 1 走到 n 的總和已經是 2n - popcount(n)，那麼這條路徑再繼續 (↙) 往左下方延伸走到 2n 的話，2n - popcount(n) + 2n = 2(2n) - popcount(2n)；如果是 (↘) 往右下方延伸的話，2n - popcount(n) + 2n+1 = 2(2n+1) - (popcount(n)+1) = 2(2n+1) - popcount(2n+1)，兩種情況都會讓遞迴式成立，故得證。
[4] 關於 digit DP 的實作細節可以參考 xxx。

實作：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57


#include <bits/stdc++.h>
using namespace std;

#define LL long long

// Given c = bitcount(x) + bitcount(y),
//       0 <= x < pow(2,a),
//       0 <= y < pow(2,b), and
//       s = x + y,
// we return the number of pairs (x, y).
inline LL digit_dp(int c, int a, int b, LL s) {
    LL dp[2][105][2] = {0};
    dp[1][0][0] = 1; int i;
    for(i=0; (1ll<<i) <= s; i++) { // look at i-th bit from the LSB when this bit does not exceed the final sum's MSB.
        memset(dp[i&1], 0, sizeof dp[i&1]);
        for(int p=0; p<=c; p++) // 先行假設進行第 i-th bit 加法之前已經使用 p 個 bit
            for(int xx=0; !xx||xx<=1&&i<a; xx++) // 決定是否挑 x 的第 i-th bit，當超過 x 的範圍時不能取
                for(int yy=0; !yy||yy<=1&&i<b; yy++) { // 決定是否挑 y 的第 i-th bit，當超過 y 的範圍時不能取
                    // dp[i&1][.][這個 entry 代表這個 i-th bit 計算完的結果是否會丟 carry bit 到下一位]
                    // 令運算前遇到的 carry bit 為 t，那麼運算後必須滿足 sum bit 的一致性：t ^ xx ^ yy == (s>>i)&1
                    // 欲求 t，可做 t ^ xx == ((s>>i)&1) ^ yy，再做 t == (((s>>i)&1) ^ yy) ^ xx
                    int t = ((s>>i)&1) ^ yy ^ xx;
                    dp[i&1][p+xx+yy][(t+xx+yy)>>1] += dp[(i&1)^1][p][t];
                }
    }
    return dp[(i&1)^1][c][0];
}

// Solution (750-G): https://codeforces.com/blog/entry/49412
// Based on the solution, given the sum s, the maximum LCA x
// satisfies: s >= (2^(L+1)+2^(R+1)-3) * x + (2^R-1).
// Note that the (a, b) we want should satisfy:
// 2a-popcount(a)-(2x-popcount(x)) + 2b-popcount(b)-(2x-popcount(x)) + x = s
// ==> 2 * (a+b) = s+3x-2popcount(x) + popcount(a)+popcount(b)
// If L=0 ==> a ∈ [x,x]; L>=1 ==> a ∈ [x<<L, (x<<L) + 1<<(L-1)); # of free bits = max(0, L-1)
// If R=0 ==> b ∈ [x,x]; R>=1 ==> b ∈ [(2x+1)<<(R-1), ((2x+1)<<(R-1)) + 1<<(R-1)); # of free bits = max(0, R-1)
// Note that if we let a = baseA + dA, where baseA := (x << L), and
//                     b = baseB + dB, where baseB := (R==0 ? x : (2x+1)<<(R-1)), then
// ==> 2 * ((baseA+dA) + (baseB+dB)) = s+3x-2popcount(x) + popcount(baseA+dA)+popcount(baseB+dB)
// ==> 2 * (dA + dB) = s+3x+popcount(baseA)+popcount(baseB)-2(popcount(x)+baseA+baseB) + popcount(dA)+popcount(dB)
// Also note that popcount(baseA)==popcount(x) and popcount(baseB)==popcount(x)+(R>=1). Therefore
// ==> 2 * (dA + dB) = s+3x+(R>=1)-2(baseA+baseB) + popcount(dA)+popcount(dB)
// ==> 2 * (dA + dB) = r + c, where 0 <= c <= max(0,L-1) + max(0, R-1)
int main() { ios_base::sync_with_stdio(false); cin.tie(nullptr); // IO 優化
    LL ans = 0, s; cin >> s;
    for (int L=0; s >= (1ll<<(L+1)) - 1; L++) // when R = 0, maximum L should satisfy s >= 2^(L+1) - 1
        for (int R=0;; R++) {
            LL x = (s - (1ll<<R) + 1) / ((1ll << (L+1)) + (1ll << (R+1)) - 3); // the maximum possible LCA
            if (x < 1) break; // given a fixed L, the maximum R should still let x > 0.
            LL r = s + 3*x + (R>=1) - 2 * ((x << L) + ((R==0) ? x : (((x<<1)|1)<<(R-1))));
            for(int c=0; c<=max(0,L-1)+max(0,R-1); c++)
                if (!((r+c)&1)) // if (r+c) is even, then:
                    ans += digit_dp(c, max(0,L-1), max(0,R-1), (r+c)>>1);
        }
    cout << ans << endl;
    return 0;
}

結果： Example image